THE ISHANGO BONE:

THE WORLD’S FIRST KNOWN MATHEMATICAL SIEVE AND TABLE OF THE SMALL PRIME NUMBERS

Abstract

This paper aims to show that the Ishango bone, one of two bones discovered in the 1950s buried in ash on the banks of Lake Edward in Democratic Republic of Congo (formerly Zaire), after a nearby volcanic eruption, is the world’s first known mathematical sieve and table of the small prime numbers. The bone is dated approximately 20,000 BC.

Key to the demonstration of the sieve is the contention that the ancient Stone Age mathematicians of Ishango in Central Africa conceived of doubling or multiplication by 2 in a more primitive mode than modern Computer Age humans, as the process of “copying” of a singular record (that is, a mark created by a stone tool as encountered in Stone Age people’s daily experience). Similarly, the doubling of any number was, by logical extension, a process of copying of any number of records (marks) denoting an integer, thereby doubling the exhibited number (marks). Some evidence for this process of “copying”  and thus representing numbers as consisting of “copies” of other numbers, is displayed on the bone and can still be found to exist in the  number systems of modern Africans in the region. 

Unlike previous speculations on the use of the bone tool by other studies, the ancient method of sieving of the small primes suggested here is notable for unifying (making use and explanation of)  all columns of the Ishango bone; whilst all numbers exhibited form an essential part of the primitive mathematical sieve described. Furthermore, it is stated that the middle column (M) of the bone inscriptions houses the calculations of the Ishango Sieve. All numbers deduced in the middle calculation column relate to a process of elimination of the non-prime numbers from the sequence of numbers 1,2,3,4,5,6,7,8,9,10 (although numbers 1 and 2 are omitted). The act of elimination is proven by the display of the numbers deduced in the middle column; namely: 4, 6, 8, 9, and 10 and the subsequent omission  of these same numbers from the following list leaving only: 5, 7   at the bottom of column M.

This elimination process described above is repeated to obtain the primes 11,13,17,19 when eliminating non-primes from the sequence 11,12,13,14,15,16,17,18,19,20. However, only calculations for the sequence 1 to 10 (for numbers above 2) are displayed in column M; as if to exemplify the Ishango Sieve method for the benefit of posterity.

1. Introduction

This paper aims to show that the Ishango bone, one of two discovered in the 1950s buried in ash on the banks of Lake Edward in Democratic Republic of Congo (formerly Zaire) after a nearby volcanic eruption [1], is the world’s first mathematical sieve and table of the small prime numbers.  This pronouncement will be greeted with astonishment in many circles, for various reasons. Firstly, it has been the established view in modern times, that Eratosthenes of Cyrene (276-194 BC), the ancient Greek director at the world-famous library at Alexandria in ancient Egypt was the inventor of the first mathematical sieve for the prime numbers on the African continent (that is, 3rd century BC Alexandria, Egypt) [2]. Yet the Ishango bone is dated as 22,000 years old by carbon dating [3]. This would mean that Central Africa precedes Greek invention of the prime sieve of Eratosthenes by at least 19,700 years! Furthermore, the discovery throws into question the Greek origins of mathematics; since the method of elimination of Eratosthenes  closely resembles that of the Stone Age Ishango mathematicians. It may well have been an idea transmitted earlier to the ancient Egyptians before the Greek conquest of Egypt. We note a similarity between the Ishango and ancient Egyptian uses of doubling used in conjunction with addition to undertake more complex mathematical tasks. The suggestion is that the Greeks merely usurped the the scientific knowledge and status of the Egyptians. It is worthy of note that Eratosthenes was the director of the library at Alexandria and therefore had access to many works, for which he could claim to be the originator. The same is true of other Greeks, such as Euclid; if, indeed they were ethnically  Greek at all, rather than Egyptian. This has never been satisfactorily substantiated.

The Ishango bone, first discovered by the Belgian Professor Jean de Heinzelin de Brouhart in the 1950s [4], is a 10 cm long curved bone which has 168 notches distributed along three columns on the bone (shown in the diagram below) which are now commonly referred to as columns G, M and D after the French terminologies for Left (Gauche), Middle (Milieu) and Right (Droite).

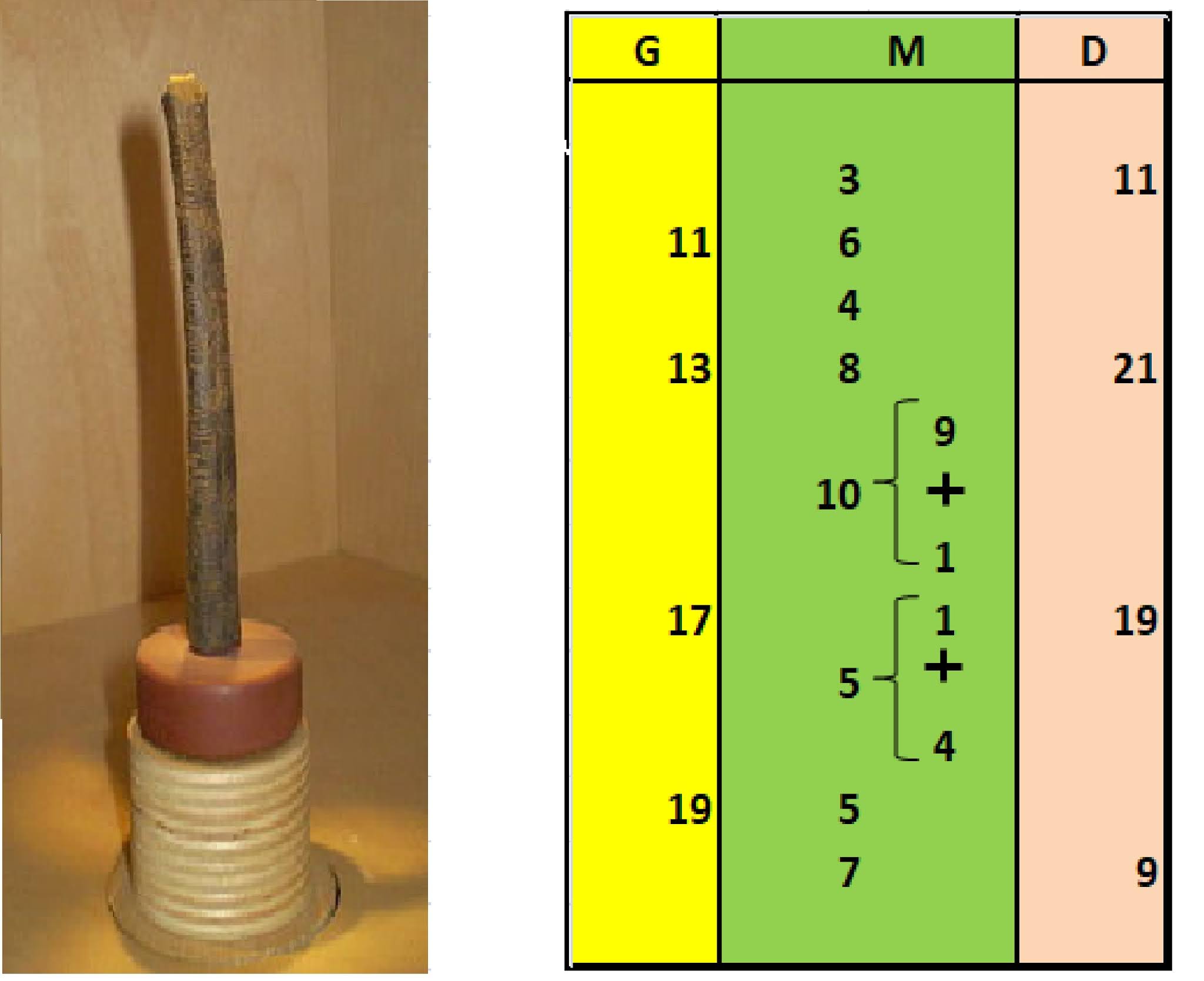Figure 1a. A Schematised Representation of the Marks on the Ishango Bone Arranged in Three Columns Left (G), Middle (M) and Right (D

Column G

Considering the columns in this same order, we note that column G is the most controversial as this column displays in sequence the four prime numbers between 10 and 20. Quite typically, the presentation of prime numbers is dismissed by most studies as fortuitous; and not the result of any deliberate or conscious reckoning of the primes. Pletser and Huylebrouck [5] are happy to assert, without justification,  that since no awareness of the primes has been previously identified before the classical Greeks, this possibility is simply eliminated. The prime sequence on the bone actually consists of six primes in sequence starting from the bottom of Column M: 5,7, continuing to column G: 11,13,17,19. In fairness to this argument for dismissing awareness of the primes, all of the primes could in fact be taken to be +1 or -1, either side of  multiples in base 6: 6, 12, 18. But this then does not explain the rationale for the quite elaborate calculations that take place in the middle column M.

Fig 1b. De Heinzelin’s Detailed Drawing of the Ishango Bone

Column M

Column M is seen to be the main column housing the calculations for the Ishango prime sieve. Here is where we see doubling  and representations of the compositions of numbers such as 10 = 5 + 5 and possibly also 10 = 9 +1  exhibited by the fact that one of the tally marks in this group is marked smaller and spaced slightly further apart from the group, possibly  to be distinct from the others.  The arrangement of the middle column displays a definite order of calculations and deductions followed by the sequence of primes presented as results, starting at the foot of the column. Throughout the top of column M we see the doubling of the numbers from 1 to 5 (with numbers 1 and 2 omitted). In the case of doubling 5 to get 10, we see a reversal of the order, so that 10 is written as 

10

5

5

This appears to be a deliberate representation of 10 =5+5, which we will revisit further ahead.

Referring to figures 1a and 1b, we notice that the columns all sum to totals that are factors of 12. Columns G and D sum to 60 = 5 x 12; whilst column M sums to a total of 48 = 4 x 12.  This factoring of twelve in the totals of the columns does not look accidental. It looks very deliberate. This has a very interesting bearing on the contention of the numbers that are fourth to last and third to last in column M: First we see the number 10 composed of 9+1 in the schematic. This is because it is contended whether or not the marks form one group. Or whether this is really nine marks followed by a doubtful mark. Similarly, for the number 5 composed of 1 + 4, only the 4 marks are very clear and bold where as the fifth mark seems to stand further apart and is not as clear. Nevertheless, because these must add up to factors of 12 (as contended here) this makes a strong case for the sum of column M not being 46, but rather being 48 (a factor of 12) and hence the 10 and the 5 being deliberately composed of 9 bold marks and by one less bold mark (further apart from the group) and in the case of the 5, 4 bold marks and 1 less bold mark, again made distinct from the group.

Column D

This column appears to display a system of numbers in the base 10. The four integers would appear to be expressions of 10+/-  1 and 20 +/- 1. Column D completes the prime sieve formed by columns G and M by setting the range of the number sequence from which to sift the primes. First, the primes in the range n = 1 to 10 are sifted (for n > 3) by a process beginning with the doubling of numbers 1 to 5 (excluding 1 and 2). Secondly, the primes in the range 10 to 20 are then sifted by a process beginning with the doubling of numbers 6 to 10. However, for purposes of economy (we suspect), only the calculations for sifting from numbers  in the range 1 to 10 are exemplified on column M. The Ishango mathematicians will have judged that one example of their sieving method sufficed.

Previous Interpretations of the Ishango Bone

Of the interpretations offered by past studies on the nature of the Ishango bone, none have managed to explain all of the facets of information exhibited by the bone or indeed given any explanation that sees all columns of the bone as dedicated to a single unified purpose.  The Study of Pletser [6] suggests that the bone exhibits a base 12 counting system. In support of this theory Pletser notes that all columns of the bone sum to factors of 12 being 60 each for the G and D columns and 48 for the M column.  It is appreciated by Pletser that column  M is central to understanding the numbering system and the arithmetic on the bone.  Hence much attention is paid to this column. But when it came to columns G and D Pletser  then engages the reader in the problem of “How to Account for the G and D Columns” as if some use needs to be discerned for them. Pletser and Huylebrouck [7], further explore the base 12 theory, but do not present a theory that sees the markings on the bone as anything more than simple  arithmetic; fitting a pre-disposed view of the limited abilities of primitive people.  Much of the data is thus unexplained and very disjointed. This is typical of much work on the interpretation of the bone. De Heinzelin [8] himself proposed that the bone represented some elementary form of arithmetic game; but this lacked sufficient correspondence with the data. The exception to this is perhaps the work of Marshack [9] who interprets the bone to be a lunar calendar and was able to demonstrate a level of correspondence between the engraved marks on the bone and astronomical lunar periods. Further support for Marshack’s theory is seen to be suggested by the fact that modern Africans still use bones, strings and other devices as lunar calendars.

2. The Negative  Pre-disposition of Mathematical Historians Towards So Called “Primitive” Societies

In the remainder of the paper the term primitive, as employed by the author will not be taken to mean “backward” – merely “ancient” and perhaps “basic” due to limitations imposed by the available tools at Stone Age man/woman’s  disposal. However, we must also deal with the more derogatory application of the term “primitive” as applied invariably to African people in the history of mathematics.

A long history of negatively predisposed scholarship on Africa in mathematics has had an impact on the failure to see merit in the mathematics and science of African people. In this section, I rely heavily on Claudia Zaslavsky’s excellent literary review  in her work “Africa Counts” of what is essentially a brief history of racism in mathematics.  Zaslavsky provides us with a snapshot of the views of of prominent scholars that had a major influence on the predisposition of scholars coming into the field of the study. Furthermore, she does this from the standpoint of a practising mathematician.

As Zaslavsky has noted: “In Great Britain there arose a school of anthropologists led by E.B. Tylor, having a point of view based on their interpretation of the new doctrine of evolution. Their thesis was this: man evolved from a primitive to an advanced state over many millennia. The white man had arrived at the highest level in contrast to the primitive savages of Darkest Africa, who were still in the very early stages of evolution. ”  [10].

Further works cited by Zaslavsky reinforce these associations of primitivity with African peoples such as the work the “Number Concept” by L.L. Conant. published in 1896 [11]. There emerged the commonplace belief in European scholarship that Africans were incapable of counting beyond a certain denomination.  She notes: “Conant sees the occurrence of numbers up to a million among South African people as remarkable exceptions”   –  to a law that basically matched intelligence to the ability to count to higher denominations [12]. 

Frank Boas, writing in the late 1930s, gives some respite from the preponderance of negative views of the intellect of African people. On encountering this same prejudice he is robust in his rejection: “As is well known, languages exist in which the numerals do not exceed 3 or 4. It has been inferred from this that people speaking these languages are not capable of forming the concept of higher numbers. I think this interpretation of the existing conditions is quite erroneous.  …just as soon as these people find themselves in contact with civilization, and when they acquire standards of value that have to be counted, they adopt with perfect ease higher numerals from other languages, and develop a more or less perfect system of counting.” [13].

We see from the quotation of Boas who is sympathetic that nevertheless, there is still the underlying supposition of the absence of civilization. Similarly, Levy-Bruhl who many might assess as yet another sympathetic scholar had a penchant for dividing humanity in terms of the “pre-logical”  mentality of “lower societies” and the “logical” mentality of civilized peoples [14].

Given this historical backdrop it is no surprise that credit is never given to anything ingenious in African culture to do with mathematics or science. In fact the topic of mathematical reasoning is never even contemplated. At most, discussions on African people will centre on methods of simple arithmetic, counting, but never abstract reasoning and mathematics. This is why mainstream scholars feel at ease with dogmatic assertions about the absence of awareness of prime numbers among African civilizations; even in the case of the treatment of ancient Egyptian mathematical achievements. For this reason, the ingenious achievements of the Ishango mathematicians in inventing the worlds first known sieve of the prime numbers has been of course overlooked.

4. Copying as a Primitive  Concept of Multiplication in Ishango Society

It has been a natural progression from the above outmoded yet still prevalent attitudes, that all research into the thinking of so called primitive societies thus far has always focused on abilities of counting and simple arithmetic. No studies known to this author to date entertain the possibility that an ancient people other than Europeans might be capable of actual mathematics and abstract thought. We have already commented on the dismissal by modern authors of the idea that prime number awareness might have existed before the classical period of the ancient Greeks. Thus we find no possible explanations or models for methods of multiplication or division in so called primitive societies in literature, since even to entertain the idea is an apparent scientific taboo. 

We are thus forced to work from first principles in order to arrive at a theory of how the Stone Age mathematicians of Ishango might have achieved the feat of multiplication by 2 or doubling by a process of copying or replicating stone tool records (marks).

It is contended here that these ancient Africans’ early concept of number was formed by their experience of recording by making a mark with a stone tool. They conceived of multiplication by 2 as the process of a number making “copies” or replicas of itself. It makes sense to expect that the concept of multiplication held by Stone Age people differs from that of modern computer age humans. In fact, their concept of multiplication by 2 would be generated from the act of making a mark, then making a copy of that singular mark to denote 2 doubled from 1. Similarly, any number of tallies made by striking marks on a bone can be doubled by making a copy of these same tallies.

To support the above contention, we note that on the Ishango bone, in the middle column M, the number 10 is clearly expressed as composed of two copies of 5, hence they are displayed immediately below 10 as below 

10

5

5

To further support this notion of numbers composed of “copies” of another number, we note the following observation by Pletser and Huylebrouck [15] in their 1999 paper: “A remarkable fact in the denominations and gestures for the numbers from 6 to 9 is that these can be formed by different principles. Sometimes 6 and 8 are expressed as 3+3 and 4+4…”. So in the demonstration of the proof of the Ishango sieve to follow, it will be seen that this conception of copying indicated above exists in societies of the region and suffices as a means of doubling numbers. Furthermore, identifying numbers that are composed of “copies” of other numbers suffices as a means of identifying composite or non-prime numbers, as we shall see shortly.

Lastly, it is curious that the Ishango mathematicians do not exhibit the numbers 1 and 2 even though these numbers are patently employed in their calculations. Is it possible that these ancient mathematicians had a sacred reverence for these numbers  which has partially hidden their ingenious sieve method for determining the small primes? For instance, the number two is used in doubling; yet nowhere is two displayed on the bone. Also the number 1, predecessor of 2, is not displayed overtly. Alternatively, it may simply be the case that as a way of shortening the length of calculations they have opted to omit the numbers and save time, effort and resources.

5. Proof of the Ishango Mathematical Sieve

Our ancient Ishango mathematicians would have begun the sieving process by first doubling all numbers 1 to 5 (1 and 2 omitted on the bone but shown here for completeness of logic)

Figure 2. The Doubling of Numbers 1 to 5

to get 2,4,6,8,10 in our second row as above  (but starting from 3 on the bone itself to double to 6).

For completeness we include all doubling from 1 upwards although this begins at 3. The third row shows the numbers produced when a number and its double are added, so that for instance, 9 is obtained from the sum of 3 and 6. We note that like all even numbers, 6 is composed of 2 “copies” of another number, 6 is composed of copies of 3 (that is 6 = 3+3 ).We note all numbers beyond 6 in the 3rd row are composed of copies of other numbers.

In our next step all numbers that are composed of  copies of others are eliminated from the series 1,2,3,4,5,6,7,8,9,10. The eliminated numbers are shown with a strike as below.

Figure 3. The Elimination of Numbers Composed of “Copies” of Others

We note above that all of the even numbers are composed of two copies of another number and so are eliminated. Also 9 = 3+6 from our calculations on column M. We also know that 6 is 2 copies of 3 and 6 = 3+3. Hence 9 = 3 + 6 = 3 + 3 + 3. Thus 9 is composed of copies of three and so must also be eliminated.

Having made all of our eliminations of numbers composed of copies we are left with 5 and 7.

So we write down our resulting sequence of primes in the series 1-10 as displayed on the bone.

5

7

In the next step the  elimination process described above is repeated to obtain the remaining primes 11,13,17,19  in column G, when eliminating non-primes from the sequence 11,12,13,14,15,16,17,18,19,20. As before, we begin by doubling; but this time we double  the numbers from 6 to 10 as below and proceed exactly as before.

Figure 4. The Doubling of Numbers 6 to 10.

So doubling 6 to 10 we get in the second row, 12,14,16,18,20. As before, the third row shows the numbers produced by a number and its double added, so that for instance, 24 is obtained from the sum of 8 and 16. By inspection of the composition of numbers previously generated by our doubling process it is plain to see that all of the even numbers are copies of others, as before. Furthermore, we also note that one odd number in the range 10-20 is also composed of copies of others. That number is 15 which the first process of doubling revealed is composed of copies of 5 since 15 = 10 + 5 = 5+5 +5. Hence we are able to eliminate all of the non-prime numbers as below.

Figure 5. The Elimination of Numbers Composed of “Copies” of Others.

So we write down our resulting sequence of primes in the series 11- 20 as 

11

13

17

19

as required.

6. Conclusion 

The Ishango prime sieve theory is perhaps the most consistent theory on the significance of the Ishango bone markings yet presented. This conclusion is based on certain results established by the proof of the Ishango mathematical sieve:-

–  All columns on the bone are employed as essential parts of the Ishango mathematical sieve

–  Every single number, every single tally on the bone, is employed by the theory of the Ishango mathematical sieve.

–    There is no single marking on the bone that is not explained by the Ishango mathematical sieve. 

–    Every number deduced in the middle calculation column (M) from the doubling  of numbers 1 to 5 (omitting 1 and 2), is a number eliminated from the sequence 1,2,3,4,5,6,7,8,9,10 (numbers 1 and 2 omitted), leaving only the prime sequence: 5, 7.  The eliminated numbers are those composed of copies of others, and are all exhibited in the column M namely: 4, 6, 8, 9, 10. 

– All missing numbers from the sequence 10-20  (namely the numbers composed of copies of others: 12, 14, 15, 16, 18, 20) are deducible from operations continuing the method of doubling from 6 to 10, as well as the results of previous doubling and additions illustrated.

Given the closeness of fit of the prime sieve theory with the data, one is bound to ask why such a simple sieve theory has not been entertained until now? We can only surmise that the negative predisposition of scholarship noted earlier in respect of ancient people and in particular Africans is to blame. How else could this have been missed?

The feat of the ancient Ishango mathematicians in devising a technique of sifting prime numbers from sequences of the natural numbers, using only the most basic tools of  addition preceded by a primitive form of multiplication is indeed remarkable. It is the hope that this paper will go some way towards according to the ingenious mathematicians of Ishango the recognition, respect and seminal position in world mathematics history that they deeply deserve.

7. References

[1]    De Heinzelin, J., Ishango, Scientific American 206, 6 June 1962, pp 105-114.

[2]    Burton, D.M.,  Elementary Number Theory, McGraw-Hill, 1998, 44-46.

[3]    Pletser, V., Does the Ishango Bone indicate the knowledge of Base 12?An Interpretation of a Pre-Historic Discovery. The First Mathematical Tool of Mankind.  https://www.researchgate.net/publication/222106237_Does_the_Ishango_Bone_Indicate_Knowledge_of_the_Base_12_AnInterpretation_of_a_Prehistoric_Discovery_the_First_Mathematical_Tool_ofHumankind.

[4]    De Heinzelin, J., Ibid.

[5]    Pletser, V. and Huylebrouck, D., The Ishango Artefact: The Missing Base 12 Link, Forma, 14, 1999, 339-346

[6] Pletser, V., Does the Ishango Bone indicate the knowledge of Base 12?An Interpretation of a Pre-Historic Discovery. The First Mathematical Tool of Mankind.  https://www.researchgate.net/publication/222106237_Does_the_Ishango_Bone_Indicate_Knowledge_of_the_Base_12_AnInterpretation_of_a_Prehistoric_Discovery_the_First_Mathematical_Tool_ofHumankind.

[7]    Pletser, V. and Huylebrouck, D., Ibid.

[8]    De Heinzelin, J., Ibid.

[9]    Marshack, A., The Roots of Civilization, McGraw-Hill, 1972. 

[10]    Zaslavsky, C., Africa Counts: Number and Pattern in African Culture, Lawrence Hill, 1973, p.10.

[11]    Zaslavsky, C., Ibid, p.9.

[12]    Zaslavsky, C., op. cit.

[13]    Boas, F., The Mind of Primitive Man, Macmillan, 1938, p.218.

[14]    Levy-Bruhl, L., How Natives Think, New York: Washington Square Press, 1966. N.B.: Dr Amon Saba Saakana has informed me on more than one occasion that Levy-Bruhl recanted on his “pre-logical” statement before his death; and this is hereby acknowledged for the record.

[15]    Pletser, V. and Huylebrouck, D., Ibid. p.343.